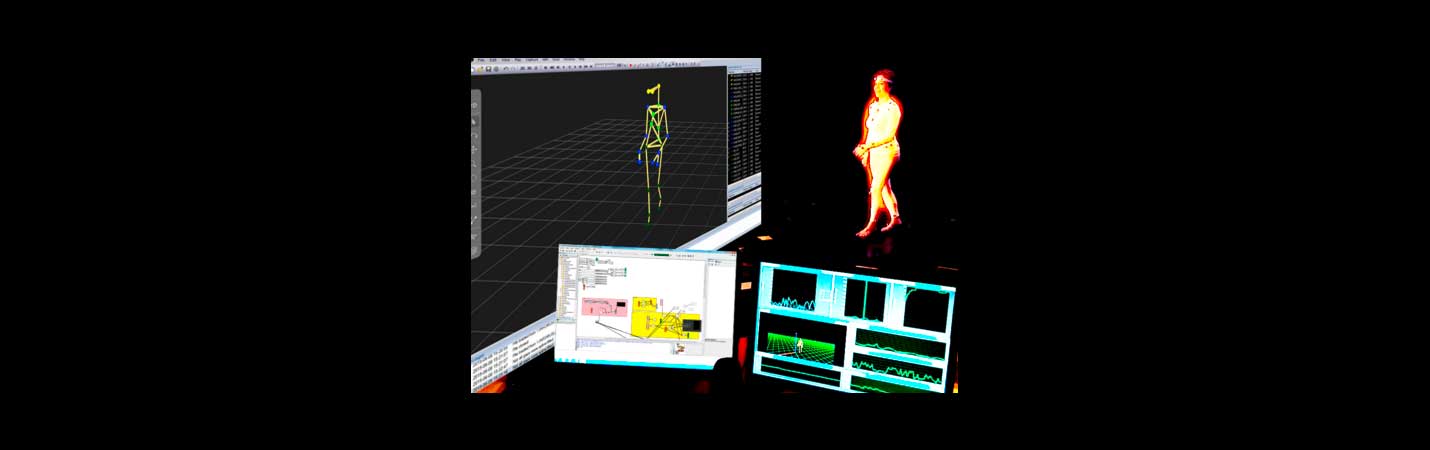
Software tools for the interactive sonification work developed in the context of the EU-ICT-H2020-DANCE (Dancing in the dark) project.
A variety of synthetic acoustical models have been designed to be informed by the following movement qualities: energy or quantity of movement, fluidity, weight and impulsiveness. Each of this synthetic approaches model the response of sounding objects, materials or natural phenomena using mathematical abstractions. The sonification approaches range from what is known as Parameter Mapping Sonification (PNSon) to Model Based Sonification (MBS).
The design of each synthesis model has been carried out in such a way that, when excited by the dancer’s activity, ensures its own transformation in a non linear fashion that conveys intuitively the characteristics and qualities of dance movement transformations.
Accordingly, in the interaction loop, the dancer perturbs these acoustic models which respond with sound and information related to the imposed energy on the system. In order to converge with the DANCE goals of the project, the synthetic models were meant to transmit the richness, complexity and realism of real world sounds. The synths are built and mapped taking into account the underlying common ground between dance and sound, and how movement qualities may also be considered in relation to the nature and articulation of sound objects. As it may happen with everyday sounds, what we listen depends on the sensorimotor coupling with an instrument or a resonating object in a way that we can possibly infer the movement from the resultant sounding morphology.
Finally, although there is always a systematic model for the way movement and sound are coupled, in order to add more realism to the interaction some small variations related to details were always added. As a result there is never an exact sonic response to the same movement.
All the sonifications were entirely written in Supercollider language. Following are the descriptions of the synthesis models employed for each movement quality.
1- ENERGY (quantity of movement):
a) An original implementation of first order dynamic stochastic sound synthesis. In this model the extracted quantity of movement of each sensor is connected to the brownian movement simulation that perturb the breakpoints of a polygonized waveform. The energy index of the dance movement is connected to the position of the elastic barriers and step size of the amplitude and duration random walks. The sonic gamut ranges from an equilibrium state with calm low and damped mechanical sounds, passing through bright clusters of bounded glissandi to more noisy entities covering the mid high registers.
b) A sound synthesis model of scrubbed rubber conveys the energy of movement injected in the system. In a nutshell, the model is comprised of an array of comb filtered sawtooth waves whose frequencies and delay times are controlled by a low frequency oscillator that generates polynomially interpolated random values . The energy index extracted from the dancer’s activity controls this random number generator. Finally, although sound spatialization may be regarded as a tangential aspect of the signification at this stage of the project, the two clusters of synthesizers are spatialized on the stereo field and assigned to each sensor.
2-WEIGHT
a) A granular synthesis model that may produce percussive sounds ranging from wood-like dabbed or light quick strokes to heavy metal drum-like percussive hits. The heaviness of the dancer’s movement is mapped across this acoustic axis. In this model a noise generator whose values are only either 1 or -1 is filtered with 18 frequencies which are exponentially distributed. This type of combination is very effective in order to produce sharp metallic sounds. Then a gaussian distribution is used to organize the percussion clouds. The more weight is put in the movement the more metallic, longer the decay and denser is the stochastic cloud of percussive sounds.
b) The model of scrubbed rubber is used again to sonify the weight quality of movement. The nature and abrupt time dynamics of the weight index produce a result way different from the one obtained in the energy index. Also In this case only one synth (instead of a cluster as in the energy model) is employed. Accordingly instead of assigning different synths to each sensor, the most relevant weight value is chosen among all sensors and thus connected to the parameters. This way all pertinent movements are sonically displayed. The acoustic result is that of clear twisted rubber friction sound which works very well with friction movements that match Laban’s wringing effort.
3-FLUIDITY
a) A resonating string model achieved based on a synthetic model of a resonating string system combining subtractive and additive synthesis. Each synthesizer is composed of a variable number of integer multiples of a fundamental. These partials are perturbed by a brownian movement generator which adds a natural and organic quality to the sound. However, the perturbation of each partial does not deviate from its center frequency by more than 2%, which leads to a spectral fusion of the tone complex into a single pitched sound. This phenomena is described by Diana Deutsch in her article concerning grouping mechanisms in music. Finally a random number generator controls the frequency range and rate of glissandi. The fluidity index connects with the parameters of the random number generator as well as with the amplitude and damping of the partials. The acoustic result moves between flowing, soft and waving glissandi when fluidity is high, and mechanical frequency changes and more metallic timbal sound entities for low fluidity. In addition the energy index is used to inform spectral brightness controlling the actual number of partials to be perceived and it’s relative amplitude.
b) A sounding liquids synthesizer which models both the vibration of surface water and underwater bubbles was originally implemented in the programming language. Fast movements, thus more keen to have less fluidity, are connected to surface water sounds while slow movements emphasize the underwater part of the model. Accordingly when the dancers move fast the acoustic response is that of splashing the liquid, while slow fluid movements produce underwater sounds since when being underwater our movements are slow and fluid. Accordingly the fluidity index control parameters such as bubble radius, density of bubbles and reverberation index.
4-IMPULSIVITY
A n additive synthesis model was employed in which the more impulsive the movements are the more harmonics the sound has. The algorithm distinguish between new impulsive movement (positive values) and stopping a repeated movement pattern (negative values). This distinction is as well sonically displayed using sharp attacks for positive values and slower attacks for negative values.